Elektronisches Geld III

Dies ist die HTML-Version der Ausarbeitung eines Vortrages im Seminar "Technische Grundlagen elektronischer Geschäftsbeziehungen" von Eike Meinders, entstanden im Wintersemester 1998/1999 am Fachbereich Informatik an der Technischen Universität Darmstadt.

Anmerkung zum Stand 2004: Die meisten der hier vorgestellten Verfahren konnten sich nicht durchsetzen und sind nicht mehr auf dem Markt. Zu Dokumentationszwecken belasse ich diese Arbeit trotzdem hier.

---

1 Einleitung

In den letzten Jahren wurden einige elektronische Geld-Systeme (auch E-Cash-Systeme genannt) entwickelt, die nicht einfach eine übertragung herkömmlicher Zahlungsmethoden auf elektronische Medien darstellen. Sie basieren also nicht auf z.B. Kreditkarten oder EC-Karten, diese Systeme werden im Vortrag "Elektronisches Geld II" vorgestellt. Es gibt eine ganze Reihe verschiedener Verfahren, einige schon ausgereift, einige nur als Vorschlag. Ein paar dieser Verfahren möchte ich vorstellen, leider würde es den Rahmen sprengen, auch nur annähernd alle Verfahren vorzustellen zu versuchen. Viele dieser Verfahren haben auch einige Gemeinsamkeiten, und ich möchte eher aufzeigen, welche verschiedenen Möglichkeiten und Ideen es im Zusammenhang mit elektronischem Geld gibt. Zu beachten ist dabei, daß keines der Systeme die Kriterien für eine Währung erfüllen, das heißt sie können kein offizielles Zahlungsmittel sein, sondern immer nur "Ersatzgeld".

Anfangen möchte ich mit den Eigenschaften, die elektronisches Geld auszeichnet bzw. auszeichnen sollte.

2 Allgemeine Anforderungen und Eigenschaften

Ein System, das einen gleichwertigen Ersatz zu herkömmlichem, "realem" Geld schaffen will, muß bestimmte Anforderungen und Eigenschaften haben, um von allen beteiligten Nutzergruppen (Staat, Banken, Händler und Privatleute) akzeptiert zu werden. Andere Kriterien sind nicht zwingend notwendig, erhöhen jedoch den Komfort, die Verarbeitungsgeschwindigkeit oder den Schutz der Privatssphäre.

Die Kriterien orientieren sich an den Eigenschaften von herkömmlichen Geld. Trotzdem muß bei elektronischem Geld neu diskutiert werden, welche Eigenschaften nötig und welche verzichtbar sind. Einige Eigenschaften werden von allen Gruppen gewünscht, bei anderen gibt es widersprüchliche Anforderungen.

Es ist aber auch aus technischen Gründen schwierig, alle Anforderungen unter einen Hut zu bekommen, und trotzdem ein praktikables System zu erhalten. Kein bisher real verwendetes Verfahren erfüllt alle Kriterien vollständig. Ein Vorschlag von Tatsuaki Okamoto und Kazua Ohta (die auch die Kriterien benannt haben, entnommen aus [1]), erfüllt alle Anforderungen, jedoch erzeugt jede Geldüberweisung ca. 200 Megabyte Daten. Ein neueres Verfahren der beiden benötigt nur noch ca. 20 Kilobytes Daten, leider habe ich keine genaue Beschreibung dieses Systems.

Die Anforderungen lauten:

2.1 Sicherheit vor Kopie und Wiedergebrauch

Dies ist eine zentrale Anforderung, die jedes ernstzunehmende E-Cash-Verfahren erfüllen muß. In E-Cash-Systemen liegt elektronisches Geld als digitales Datenpaket auf einem Computer und ist somit prädestiniert dafür, kopiert zu werden. Im Gegensatz zu Papiergeld oder Münzen ist eine digitale Kopie nicht unterscheidbar vom Original, das Verfahren muß also in irgendeiner Form dafür sorgen, daß kopiertes digitales Geld nicht ausgegeben werden kann. Diese Eigenschaft von elektronischem Geld nennt man das "Double Spending-Problem".

Auch der Wiedergebrauch des Geldes muß berücksichtigt werden. Bei Papier- oder Münzgeld gibt man den "Wertträger" beim Ausgeben stofflich weiter, so daß man ihn nicht zweimal ausgeben kann, ohne ihn vorher zu kopieren. Beim Weitergeben von digitalen Daten geschieht das Kopieren aber meist schon implizit. Hier greifen meist aber die Vorrichtungen gegen "normales" Kopieren.

Da "vernünftige" E-Cash-Verfahren kryptographische Algorithmen verwenden, hängt ihre Sicherheit generell auch von der Sicherheit dieser Algorithmen ab, auch von der verwendeten Schlüssellänge.

2.2 Ortsunabhängigkeit

Der Wert von elektronischem Geld sollte, genau wie bei realem Geld, nicht an einen bestimmten Ort gebunden sein. Es sollte von einem Computer zum Anderen transportiert werden können, auch über Netzwerke wie das Internet.

2.3 Anonymität

Es sollte Unbefugten nicht möglich sein, aus Finanztransaktionen Rückschlüsse darüber zu ziehen, welche Waren ein Kunde einkauft oder wo er einkauft. Dabei gibt es aber grundsätzlich verschiedene Standpunkte, wer befugt ist. Regierungen und Sicherheitsorgane möchten illegale Geschäfte erkennen und verhindern, Händler möchten Kundenprofile anlegen können. Dagegen möchten Privatleute Geld ausgeben können, ohne ihre Identität preiszugeben, so wie dies mit herkömmlichem Geld möglich ist.

Es gibt verschiedene Arten von Anonymität, nämlich die Anonymität des Kunden gegenüber einem Händler, die Anonymität des Kunden gegenüber der Bank und die Anonymität des Händlers gegenüber der Bank.

2.4 Off-Line Fähigkeit

Bei einer elektronischen Geldzahlung sollte es nicht nötig sein, eine Verbindung zu einem Dritten aufzunehmen, beispielsweise einer Bank. Dies erhöht die Transaktionskosten, was insbesondere für kleinen Geldgeschäften unökonomisch ist.

Die Bezeichnung "Off-Line" ist hier vielleicht etwas mißverständlich, da sie sich nicht auf die Verbindung der Teilnehmer eines E-Cash-Systems zum Netzwerk bezieht, sie hat sich aber eingebürgert. Ohne eine solche Verbindung ist natürlich generell keine Geldtransaktion möglich.

2.5 übertragbarkeit

Elektronisches Geld sollte von einem Nutzer zum anderen übertragbar sein, nicht nur an Händler.

2.6 Teilbarkeit

Eine Geldmenge sollte bis zu einem gewissen Grad in kleinere Beträge teilbar sein, und nicht nur als Block wieder ausgegeben werden können.

3 Allgemeine E-Cash-Verfahren

In diesem Kapitel geht es um E-Cash-Systeme, die den Anspruch haben, umfassend für alle Arten von elektronischen Geschäften einsetzbar zu sein. Auf Systeme, die über keinerlei kryptographische Absicherungen verfügen wie z.B. First Virtual, gehe ich nicht ein. Das NetCash-Verfahren stelle ich als erstes vor, denn es implementiert eine Art "Basisverfahren", das die typischen Elemente eines E-Cash-Verfahrens enthält. Das als nächstes beschriebenen DigiCash beispielsweise baut auf dem selben Grundschema auf, deshalb möchte ich dort in erster Linie auf die neuen Elemente eingehen. Es gibt noch weitere Verfahren, die auf dem gleichen Grundprinzip beruhen, zum Beispiel IBM iKP und NetBill, auf die ich aber nicht eingehen möchte.

3.1 NetCash

Eines der ersten E-Cash-Verfahren ist NetCash ([3]). Es wurde von B. Clifford Neuman und Gennady Medvinsky von der University of Southern California entwickelt und schon im Mai 1994 erstmals in einem Feldversuch erprobt. Es steht im Zusammenhang mit dem NetCheque-Verfahren für elektronische Schecks, das vom gleichen Team entwickelt wurde.

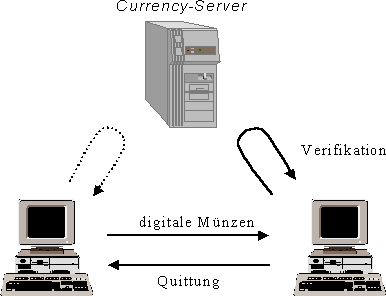
NetCash basiert auf digitalen Münzen, von NetCash "Coupons" genannt, die von sogenannten "Currency-Servern" signiert und ausgegeben werden. Diese Currency-Server können von Banken betrieben werden, die vom Staat eine Ermächtigung zur Coupon-Erzeugung bekommen haben.

Die Coupons bestehen aus einem Bitstring, der folgende Daten enthält:

• Currency-Server-Id
• Verfallsdatum
• Seriennummer
• Wert des Coupons

Dazu kommt eine digitale Signatur, mit der der ausgebende Currency-Server für die Echtheit des Coupons einsteht. Die Signatur entsteht mit Hilfe eines Public-Key-Verfahrens, so daß sie mit dem öffentlichen Schlüssel des Currency-Servers überprüft werden kann.

Möchte ein Kunde neue Coupons erwerben, alte mit abgelaufenen Verfallsdatum umtauschen oder Coupons auf sein Konto einzahlen, packt er die Coupons oder einen digitalen Scheck zusammen mit den Handlungsanweisungen und einem Schlüssel zusammen. Diese Paket verschlüsselt er mit dem öffentlichen Schlüssel des Currency-Servers und schickt es an denselben. Der Currency-Server entschlüsselt das Paket mit seinem privaten Schlüssel und analysiert den Inhalt. Wenn Coupons enthalten sind, überprüft er sie mit Hilfe der Signatur auf Betrug. Außerdem speichert er die Seriennummer in einer Datenbank, so kann das doppelte Ausgeben erkannt werden. Dabei hilft auch das Verfallsdatum, da der Currency-Server so keine Seriennummern von Coupons aufbewahren muß, die älter als ein bestimmter Zeitraum sind. Traten keine Unregelmäßigkeiten auf, erzeugt der Currency-Server neue Coupons oder einen digitalen Scheck, verschlüsselt die Antwort mit dem vom Kunden übermittelten Schlüssel und schickt sie zurück.

Es ist auch möglich, daß die Münzen von einem anderen Currency-Server erzeugt werden, dann läuft ein Clearing zwischen den beiden Currency-Servern ab. Dazu kann dann dasselbe Verfahren verwendet werden.

Wenn Kunden gegenseitig elektronische Münzen austauschen möchten, oder ein Kunde etwas bei einem Händler bezahlen will, kommt folgendes Protokoll zum Einsatz:

1. Vorausgesetzt wird eine verschlüsselte Verbindung. Die Schlüssel dafür können entweder durch einen Diffie-Hellman-Schlüsselaustausch zustande kommen, oder man verwendet ein Public-Key-Verfahren.
2. Der Sender schickt die Coupons zusammen mit einer Session-Id verschlüsselt zum Empfänger.
3. Der Empfänger verwendet das oben beschriebene Verfahren zur Kommunikation mit dem Currency-Server, um die Coupons einzuzahlen oder zu überprüfen, d h. gegen Coupons einzutauschen.
4. Waren die Coupons gültig, schickt der Empfänger eine digital signierte Quittung über die verschlüsselte Verbindung zurück an den Sender.

Bewertung

Wie man sieht, ist der Wert der digitalen Münzen in gewisser Weise unabhängig vom Aufbewahrungsort, da die Coupons ja nur einen Bitstring darstellen. Ihren Wert besteht darin, daß sie bei einem Currency-Server eingelöst werden können, dies verhält sich ähnlich wie bei herkömmlichem Geld. Auch die übertragbarkeit ist durch das Austauschverfahren gewährleistet. Die Authenzität der Coupons wird durch die Signatur gewährleistet, die der Currency-Server erzeugt. Der Kopierschutz und der Schutz vor doppeltem Ausgeben beruht auf der Seriennummer, die nur durch den Currency-Server überprüft werden kann. Dies bedeutet, daß bei jeder Transaktion eine Verbindung zum Currency-Server aufgebaut werden muß, wenn nicht auf den Kopierschutz verzichtet wird. Außerdem kann ein Kopieren zwar erkannt, aber nicht verhindert werden. Es läßt sich auch nicht erkennen, wer der Betrüger war, wenn ein Coupon zweimal beim Currency-Server eingereicht wird. Verliert ein Kunde Coupons oder werden sie ihm gestohlen, kann der Currency-Server sie ihm erneut ausstellen, da der Server ja anhand seiner Aufzeichnungen nachvollziehen kann, daß der Kunde den Coupon vorher einmal besessen hat. Das Risiko, daß die Münzen möglicherweise inzwischen vom Dieb ausgegeben wurden, trägt jedoch der Kunde selbst.

Die Teilbarkeit ist indirekt gegeben. Die Coupons selbst lassen sich zwar nicht teilen, jedoch können sie beim Currency-Server gegen neue Coupons eingetauscht werden. Dazu ist aber eine Kontaktaufnahme mit dem Currency-Server notwendig.

Anonymität ist normalerweise nicht vorhanden. Der Currency-Server kann einzelne Coupons anhand der Seriennummer identifizieren und mit dem Namen der Ein- und Auszahler verbinden (Tracking). So kann der Currency-Server ein Profil des Kunden erstellen. Das funktioniert aber nicht mehr so einfach, sobald die Coupons über mehrere Currency-Server getauscht werden, da jeder Server dann nur noch eine Ausschnitt der Informationen hat. Unterlaufen können die verschiedenen Server dies, indem sie gegenseitig die Tracking-Informationen austauschen.

Der Empfänger einer Zahlung, also zum Beispiel ein Händler, hat normalerweise keine Möglichkeit, etwas über seinen Kunden zu erfahren, es sei denn, er "konspiriert" mit dem Currency-Server.

3.2 DigiCash

Der Kryptograph David Chaum entwickelte Ende 1994 das ecash-System, und gründete zum Zwecke seiner Vermarktung die Firma DigiCash ([4]). Sein System konnte sich zwar am Markt nicht durchsetzen, obwohl ihm einmal eine große Zukunft vorausgesagt wurde. Die letzte mir zur Verfügung stehende Information über DigiCash lautet, daß ein Konkursverfahren läuft und DigiCash nach Geldgebern sucht. Trotzdem möchte ich auf DigiCash ecash eingehen, da es einige interessante Features hat.

Im DigiCash-System hat jeder Kunde einerseits einen spezielles Bankkonto für DigiCash-Geld, andererseits eine "Geldbörse" (Wallet) für DigiCash-Münzen auf seinem Computer. Das System ähnelt in gewisser Weise dem NetCash-Verfahren, mit der Bank als Currency-Server und der gleichen Zusammensetzung der digitalen Münzen. Es gibt jedoch eine bedeutende Erweiterung: Wenn die digitalen Münzen vom Konto abgehoben und in die persönliche Geldbörse übertragen werden, wendet die Bank verdeckte Unterschriften (Blind Signatures, von David Chaum erfunden, siehe auch [5]) an. Im Gegensatz zu normalen digitalen Signaturen sieht der Unterzeichner hier nicht, was er unterschreibt. Dies verhält sich analog zu einem verschlossenen Umschlag, der einen Geldschein und Kohlepapier enthält. Die Bank drückt auf den Umschlag einen Stempel, eben die Signatur, der besagt, daß die Bank den Inhalt für einen gültigen Geldschein mit einem bestimmen Wert erklärt. Der Kunde entfernt den Umschlag und das Kohlepapier, und hat einen von der Bank unterschriebenen Geldschein, den die Bank nicht selbst gesehen hat. Auf die digitalen Münzen übertragen bedeutet dies, eine Münze wird mit einem Blendungsfaktor versehen, und die Bank signiert die verdeckte Münze. Dabei wählt sie den geheimen Schlüssel derart, daß sie später aus der nicht verdeckten signierten Münze wieder erkennen kann, welchen Wert sie signiert hatte. Der Kunde bekommt die Münze zurück, kürzt den Blendungsfaktor wieder heraus und erhält so die signierte Münze.

Dieses Protokoll hat den Zweck, daß die Bank die Seriennummer beim Ausgeben der Münzen nicht erkennen kann und so keine Zuordnung von Münzen zu Besitzern vornehmen kann. Beim Einzahlen von Münzen gibt es keine solche Verschleierung: Die Bank erkennt, wer Münzen auf seinem Konto einzahlt. Die Begründung hierfür ist, daß man auf diese Weise der Geldwäsche einen Riegel vorschieben möchte, indem es keine Anonymität für Händler gibt. Empfänger von Zahlungen sind auch gezwungen, Münzen sofort einzuzahlen und dafür eine Online-Verbindung zur Bank aufzubauen, weil sie sonst keinerlei Sicherheit über die Gültigkeit der Münzen haben. Auch hier gibt es nämlich keinen Schutz vor Kopieren und doppeltem Ausgeben von Münzen, sondern nur eine Erkennung desselben, da das gleiche Seriennummern-Verfahren wie bei NetCash verwendet wird. Für die Kunden genügt es jedoch, ihre Geldbörse zu füllen, sie müssen sonst keine Verbindung mit der Bank, sondern nur mit dem Händler aufnehmen.

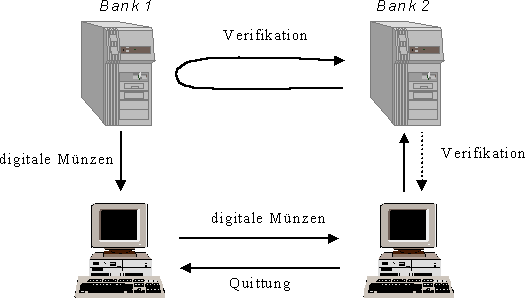
Die Münzen sind nur in bestimmten Größen erhältlich, die exponentiell wachsen, also z.B. 1 DM, 2 DM, 4 DM, 8 DM usw. Alle Summen müssen aus diesen Münzen zusammengesetzt werden. Hat ein Kunde die passenden Münzen nicht in seiner Geldbörse, muß er vor einer Bezahlung Kontakt mit seiner Bank aufnehmen und neue Münzen von seinem Konto abheben. Wird eine Rechnung mit DigiCash bezahlt, besteht der Gesamtbetrag also möglicherweise aus vielen einzelnen Münzen, und jede muß einzeln übertragen werden.

Der Vorteil der Blind Signatures liegt darin, daß der DigiCash Kunde anonym bleiben kann, wenn er es wünscht. Dieses Feature bieten die meisten anderen E-Cash-Systeme nicht, so ist es schade, daß es so aussieht, als würde DigiCash wieder verschwinden.

3.3 Eine bessere Lösung für das Double Spending-Problem

Dies ist kein vollständiges E-Cash-System, sondern ein von Bruce Schneier in [1] vorgeschlagener Ansatz, besser mit dem Double Spending-Problem umzugehen. Bei den bisher beschriebenen Verfahren gibt es ja für digitales Geld eine Seriennummer, die von einer Bank oder ähnlichem gespeichert werden muß. Damit kann man zwar erkennen, wenn versucht wird, elektronisches Geld zweimal auszugeben. Es bleibt jedoch offen, ob der Kunde oder der Händler der Betrüger war, und im Falle von anonym bleibenden Kunden läßt sich dieser auch nicht ermitteln, falls er des Betruges verdächtigt wird. Dieses Manko versucht das folgende Verfahren zu beheben.

Für eine Transaktion erzeugt der Kunde einen ihn identifizierenden String I. Diesen dupliziert er k mal und teilt jeden dieser Strings I_k mit Hilfe eines Secret-Splitting-Verfahrens verschieden auf, d.h. es entstehen k verschiedene Stringpaare (I_kL,I_kR), die jeweils miteinander verXORt den String I ergeben. Diese Stringpaare I_k enthalten also die Identifikation des Kunden, die aber nur gelesen werden kann, wenn beide Teile vorliegen. Sie werden an die digitale Münze gehängt und von der Bank überprüft und signiert. Wenn der Kunde die Münze an einen Händler übermitteln will, bekommt er von diesem einen zufällig gewählten Bitstring mit k Bits. Nach diesen Bits muß er jeweils den linken oder den rechten Teil der I_k wählen, und nur der gewählte Teil wird mit der Münze an den Händler übermittelt. Dabei ist durch die Signatur der Bank gewährleistet, daß der Kunde nicht mogeln kann und dem Händler die falsche Hälfte eines I_k übermittelt. Im Normalfall, also wenn die Münze nicht doppelt ausgegeben wird, kann sowohl der Händler als auch die Bank mit der vorliegenden Information nicht den Kunden identifizieren. Die Bank speichert aber neben der Seriennummer auch die Identifikations-Teilstrings.

Reicht ein Händler bei der Bank eine Münze ein, deren Seriennummer die Bank schon in ihrer Datenbank hat, und die Identifikations-Teilstrings sind gleich, so weiß sie, daß der Händler die Münze kopiert haben muß. Sind die Identifikations-Teilstrings verschieden, war der Kunde der Betrüger, denn bei verschiedenen Zahlungsvorgängen, auch mit der gleichen Münze, bekommt der Kunde verschiedene Selektor-Bitstrings vom Händler. Außerdem wird sich dann ein k finden lassen, bei dem der Kunde einmal den linken und einmal den rechten Teilstring verwenden mußte, so daß sich daraus der volle Identifikationsstring ermitteln läßt.

Der einzige Schwachpunkt dieses Verfahrens liegt in der Tatsache, daß es jemandem gelingen könnte, sich in die Verbindung zwischen dem Kunden und dem Händler einzuschleichen und die Münze zu kopieren. Wenn er schnell genug ist und die Münze vor dem Händler bei der Bank einlöst, gibt es mit diesem Protokoll aufgrund der Anonymität keine Möglichkeit zu verhindern, daß der Händler als Betrüger dasteht und nicht zu seinem Geld kommt. Trotzdem ist dies ein interessanter Ansatz, der meines Wissens aber in keinem kommerziellen E-Cash-System verwendet wird.

4 Micropayment-Verfahren

Die bisher vorgestellten Verfahren wurden unter dem Gesichtspunkt besonderer Sicherheit entwickelt. Dabei wurde häufig in Kauf genommen, daß einzelne Geldtransaktionen verhältnismäßig aufwendig sind und selbst wieder durch benötigte Computer-Rechenleistung und Netzbandbreite einen nicht vernachlässigbaren Geldbetrag kosten. Dies fällt bei größeren Zahlungen nicht so stark ins Gewicht, wenn dafür die Sicherheit gewährleistet ist. Ein ähnliches Problem ergibt sich auch bei herkömmlichen Zahlungssystemen, etwa bei Kreditkarten. Die Transaktionskosten sollten also in einem angemessenen Verhältnis zur übertragenen Geldsumme stehen.

Unter einer gewissen Schwelle, also z.B. bei Beträgen unter 1 DM, stimmt dieses Verhältnis bei den allgemeinen E-Cash-Verfahren nicht mehr, es werden spezielle übertragungsverfahren für kleine Geldsummen benötigt, eben Micropayment-Verfahren. Wo diese Schwelle liegt, hängt natürlich stark vom jeweiligen Verfahren ab. Spätestens im Pfennigbereich sollte nach derzeitiger allgemeiner Einschätzung ein Micropayment-Verfahren eingesetzt werden, dies könnte sich aber natürlich in Zukunft ändern, wenn Rechenleistung, Speicherplatz und Netzbandbreite sich weiter verbilligen.

Besondere Bedeutung sehen die Entwickler von Micropayment-Verfahren in der Kommerzialisierung des Internets. Sie sehen eine Entwicklung voraus, bei der Online-Angebote nicht mehr kostenlos zu erhalten sind, sondern bezahlt werden müssen, beispielsweise ein paar Pfennige für einen Artikel in einem Online-Nachrichtenmagazin.

Um die Transaktionskosten zu drücken, müssen an irgendeiner Stelle Einschränkungen gemacht werden. Häufig ist der Preis eine etwas geringere Sicherheit, die Entwickler argumentieren dann damit, daß es bei den geringen Geldmengen akzeptabel ist, wenn etwas davon verlorengeht. Außerdem geht man davon aus, daß keiner Betrug begehen wird, wenn die Kosten dafür höher sind als der Wert der Beute.

Technisch gesehen geht es darum, Rechenleistung zu sparen, beispielsweise indem zeitaufwendige Public-Key-Signaturen durch einfach zu berechnende kryptographische Hash-Funktionen ersetzt werden. Die RSA-Signaturerzeugung beispielsweise ist ca. 10000 Mal langsamer als typische Hashfunktionen wie MD-5, und die RSA-Signaturverifikation ist immer noch ca. 100 Mal langsamer [6]. Auch Netzbandbreite läßt sich sparen, indem das Protokoll möglichst minimiert wird und vor allem Verbindungen mit nur indirekt am Geschäft beteiligten (Banken, Verifizierungsstellen) vermieden werden.

Es gibt eine ganze Reihe von völlig verschiedenen Ansätzen, diese Probleme zu lösen. Einige von ihnen werde ich im folgenden vorstellen. Teils handelt es sich um bereits kommerziell eingesetzte Systeme, teils um noch nicht praktisch umgesetzte Vorschläge.

4.1 Millicent

1995 entwickelte Mark Mansasse am System Research Center der Firma Digital (inzwischen Compaq) Millicent ([7]). Es wurde für Transaktionen mit Geldbeträgen entworfen, die kleiner als ein Cent sind und ist eines der ersten speziellen Micropayment-Verfahren.

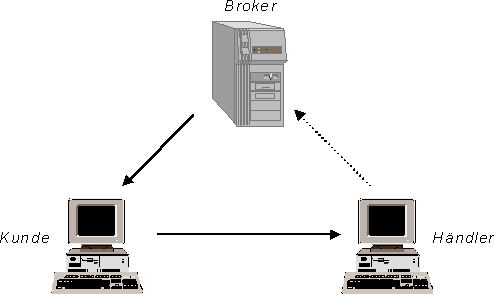
Die Teilnehmer des Millicent-Systems sind Kunden, Händler und Vermittler (Broker). Die Händler unterscheiden sich von den normalen Kunden dadurch, daß sie eigene digitale Münzen herausgeben, die nur bei ihnen gültig sind und speziell für einen Kunden hergestellt werden. Diese Münzen heißen im Millicent-Jargon "Scrip".

Um bei einem Händler einkaufen zu können, erwirbt ein Kunde Scrip dieses Händlers. Er kann eine größere Menge auf Vorrat einkaufen, oder nur für den aktuellen Bedarf. Normalerweise wird das Scrip nicht direkt vom Händler verkauft, sondern von einem Broker, der mehrere Händler vertritt. Zu diesem Zweck benötigt der Kunde ein Konto bei dem Broker, dieser kann auch Scrip von ihm nicht bekannten Händlern vermitteln, indem er andere Broker einschaltet. Zum eigentlichen Kaufzeitpunkt übermittelt der Kunde das Scrip in der benötigten Menge an den Händler. Dieser kann direkt selbst dessen Gültigkeit überprüfen, da er ja selbst Erzeuger des Scrips ist. Eine Quittung ist nicht vorgesehen, stattdessen schickt der Händler direkt den gekauften Gegenstand, z.B. eine Webseite, an den Kunden. Um zu seinem Geld zu kommen, reicht der Händler das wieder eingenommene Scrip an den Broker ein, der dafür Geld auszahlt.

Der Inhalt eines Millicent Scrip ist ähnlich zu den Netcash-Münzen, jedoch gibt es statt einer Bank- oder Curency-Server-Id eine Id des Händlers und des Kunden. Seriennummer, Verfallsdatum und Wert gibt es auch in Millicent und werden prinzipiell auch gleich verwendet. Auch Signaturen gibt es, die im Gegensatz zu Netcash nicht mit einem Public-Key-Verfahren gebildet wird, sondern aus Effizienzgründen aus dem Hashwert der mit einem Schlüssel zusammengesetzten Münze besteht. Als Hashfunktion könnte jede beliebige kryptographische Hash-Funktion verwendet werden.

Möchte der Kunde ein Scrip signieren, um damit zu bezahlen, ist der angesprochene Schlüssel das sogenannte "Customer Secret" , daß nur dem Kunden und dem Händler bekannt ist. Damit der Händler das Customer-Secret nicht für jeden Kunden speichern muß, wird es aus der Id des Kunden generiert. Die geschieht folgendermaßen: Der Händler besitzt einen nur ihm bekannten Schlüssel, das "Master Customer Secret". Mit den letzten vier Bit der Kunden-Id wird ein Teil des Master-Customer-Secret ausgewählt und zusammen mit der gesamten Kunden-Id gehasht. Dieser Hashwert bildet dann das Customer-Secret, das der Händler dann dem Kunden übermittelt (es reicht, wenn dies beim ersten Einkauf des Kunden bei dem Händler geschieht, ein genaues Verfahren ist nicht festgelegt). Der Kunde kann es dann zum Signieren verwenden, und der Händler kann die Signatur überprüfen, indem er sie mit seinem eigenen Ergebnis der beschriebenen Funktion vergleicht.

Die digitale Signatur des Händlers, die er direkt nach dem Erzeugen von Scrip anbringt, funktioniert ganz ähnlich. Hier kommt ein anderer, nur ihm bekannter Schlüssel ins Spiel, das "Master Scrip Secret". Damit kann der Händler, entweder mit der gleichen oder einer anderen Hashfunktion einen Schlüssel errechnen, mit dem er das Scrip signiert.

Prinzipiell ist die Möglichkeit vorgesehen, daß auch Broker Scrip für die von ihnen vertretenen Händler erzeugen können. Dazu müssen sie Master-Customer-Secret und Master-Scrip-Secret des Händlers kennen. Dies erfordert natürlich größeres Vertrauen zwischen Händler und Broker als normalerweise nötig.

Bewertung

Der Nachteil der Verwendung von Hashfunktionen für digitale Signaturen liegt natürlich darin, daß nur derjenige die Signatur überprüfen kann, der die verwendeten geheimen Schlüssel kennt. Bei Public-Key-Verfahren kann der Teil des Schlüssels, der zum Entschlüsseln dient, veröffentlicht werden, so kann jeder die Signatur überprüfen. Im Millicent-System kann aber noch nicht einmal der Kunde die Signatur des Händlers überprüfen!

Die Entwickler haben sich aus zwei Gründen für Händler-spezifische Münzen entschieden:

1. Es ermöglicht ein sehr einfaches Protokoll ohne überflüssige Kommunikation zwischen Kunden, Händlern und Brokern. Während des eigentlichen Bezahlvorgangs muß zur Verifikation des Scrips keine Verbindung zu einer Bank oder einem Broker aufgenommen werden, der Händler überprüft sein Scrip selbst.
2. Das System ist sehr gut skalierbar. Jeder Händler ist nur für seine eigenen Transaktionen verantwortlich, die Liste der bereits ausgegeben Münzen bleibt dadurch wesentlich kleiner als bei einem zentral organisierten System.

Die Anonymität von Millicent ist generell sehr begrenzt, da Scrip speziell von einem Händler für einen Kunden produziert wird. Allerdings wäre es denkbar, daß Broker eine Art "Sammelkonto" für anonyme Kunden anbieten. Händler könnten dann diese Kunden nicht mehr unterscheiden, der Broker aber natürlich schon.

Der Hauptnachteil des Millicent-Systems ist, daß es nur bei Langzeitbeziehungen zwischen Kunden und Händlern vernünftig funktioniert. Nur einmal ein Scrip mit sehr geringem Wert zu kaufen ist einfach zu aufwendig, vor allem wenn dies immer wieder mit immer wechselnden Händlern vorkommt. Effizient ist Millicent erst dann, wenn man immer auf Vorrat Scrip für einen Händler einkauft.

4.2 CyberCoin

CyberCoin ist das Micropayment-System der Firma CyberCash ([8]), die 1994 von William Melton und Daniel Lynch gegründet wurde. CyberCash ist auch der Name des von dieser Firma entwickelten, Kreditkarten-basierten E-Cash-Systems.

Es gibt im CyberCoin-System keine digitalen Münzen oder ähnliches, die über das Netzwerk transportiert werden, auch wenn der Name dies andeutet. Das Geld des Kunden bleibt auf einem speziellen Bankkonto. Wenn der Kunde es ausgeben möchte, schickt er dem Empfänger des Geldes seine Kontonummer und eine Genehmigung, einen bestimmten Betrag abzuheben. Der Empfänger wendet sich damit an den zentralen CyberCoin-Server, der das Geld vom Konto des Senders auf das des Empfängers überweist. Dieser Ansatz entledigt den CyberCoin-Kunden der Sorge, daß er sein Geld verlieren könnten, da das Geld auf dem Bankkonto aufbewahrt wird und hier die gesetzlichen Regelungen zu Bankkonten greifen. Im Gegensatz zum Millicent-System wird nicht zwischen Händlern und "normalen" Kunden unterschieden

Die Genehmigungs-Nachrichten, die ein Kunde verschickt, werden natürlich digital signiert. Dazu wird ein ganz ähnliches System wie bei Millicent verwendet, nämlich Hash-Funktionen (MD-5) in Verbindung mit zwei geheimen Basisschlüsseln D und S, die nur dem Kunden und dem CyberCoin-Server bekannt sind. Zum Verschicken dieser Schlüssel wird allerdings ein Public-Key-System verwendet.

Der Schlüssel D muß in regelmäßigen Abständen erneuert werden und dient dazu, Transaktions-Id zu generieren. Der Schlüssel S wird zusammen mit einer Transaktions-Id gehasht, dieser Hashwert ergibt einen Schlüssel, der zum Verschlüsseln einer Nachricht mit DES dient. Weil der CyberCoin-Server die Basisschlüssel ebenfalls bekannt sind, kann er den DES-Schlüssel ausrechnen und die Nachricht entschlüsseln

Eine Kauf von Daten über CyberCoin läuft nun folgendermaßen ab:

1. Der Händler schickt dem Sender nach der Einigung über das Geschäft einen Hashwert der verkauften Daten
2. Der Käufer packt seine Id, den Geldbetrag der Transaktion und den vorher empfangenen Hashwert zusammen. Die ganze Nachricht wird signiert, indem der Sender an alle Felder der Nachricht seinen Schlüssel S hängt und alles zusammen mit MD-5 hasht. Alles wird wie vorher beschrieben mit DES verschlüsselt.
3. Der Händler kann die Nachricht nicht entschlüsseln, hängt aber seine eigene digitale Signatur an und schickt alles dem CyberCoin-Server.
4. Der CyberCoin-Server kann die Nachricht des Käufers entschlüsseln und überprüft die Signaturen des Kunden und des Händlers. Ist die Transaktion gültig, schickt er dem Händler eine Quittung, die mit Hilfe des Schlüssels des Händlers signiert wird.
5. Der Händler empfängt die Quittung und schickt dem Käufer die Daten.
6. Der Käufer überprüft die Daten. Dann bildet er davon wieder einen Hashwert und schickt diesen mit einer signierten Empfangsbestätigung an der CyberCoin-Server.
7. Der CyberCoin-Server überweist das Geld.

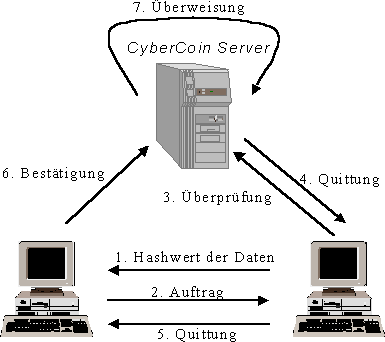
Das Verfahren sieht recht kompliziert aus, aber alle Berechnungen sind verhältnismäßig einfach. Allerdings muß bei einer Transaktion immer der zentrale CyberCoin-Server eingeschaltet werden, was erstens aus Performance-Erwägungen ungünstig ist, und zweitens jegliche Anonymität verhindert.

Das Kriterium der Ortsunabhängigkeit ist hier etwas schwierig anwendbar, weil der Kunde sein Geld ja nicht selbst aufbewahrt. Der Kunde kann aber von überall mit CyberCoin bezahlen, sofern er einen Netzzugang hat. Beim Bezahlen wird immer der passende Betrag abgehoben, so daß sich das Problem der Teilbarkeit gar nicht stellt.

4.3 PayWord

Inspiriert von Millicent, stellten Ronald Rivest und Adi Shamir, Miterfinder des RSA-Systems, 1996 zwei Micropayment-Verfahren vor: PayWord und MicroMint ([9]). Die Verfahren werden bisher nicht in kommerziellen Systemen eingesetzt, sondern stellen einen neuen Ansatz zum Micropayment dar.

Das PayWord-Verfahren verwendet die Eigenschaft der Unumkehrbarkeit von kryptographischen Hash-Funktionen, um digitale Münzen zu authentifizieren. Die Idee besteht darin Hashwert-Ketten zu verwenden, also x₁ = h(x₀), x₂ = h(x₁) = h(h(x₀)) usw. Diese Ketten lassen sich so in der Reihenfolge x₀, x₁,x₂,... sehr leicht erzeugen, jedoch in der umgekehrten Reihenfolge nicht.

Im PayWord-System stellt ein Broker einem Kunden in regelmäßigen Abständen ein digital signiertes Zertifikat aus, aus welchem ein x₀ für den Beginn der Hashwert-Kette generiert werden kann. Für einen Bezahlvorgang wird ein Startwert festgelegt, ab dem die Hashwerte rückwärts als digitale Münzen ausgegeben werden. Der Empfänger kann nachher leicht die Gültigkeit der Münzen überprüfen, da er nur prüfen muß, ob der Hashwert der Münze gleich der vorherigen Münze ist. Niemand ist jedoch ohne das Zertifikat in der Lage, aus einer Münze die nächste gültige Münze zu berechnen, weil die Hashfunktion eben nicht umkehrbar ist.

PayWord läßt sich auch als eine Art Ersatz für das in anderen Systemen weitverbreitete Seriennummer-Verfahren sehen. Die Sicherheit von Hashwert-Ketten ist natürlich höher als bei Seriennummern, die womöglich auch noch einfach durchnumeriert sind.

4.4 MicroMint

MicroMint ist zweite von Rivest und Shamir in [9] vorgestellte Verfahren. Die Grundidee ist, die Eigenschaften einer staatlichen Münzerei nachzuahmen. Die Herstellung von echten Geldmünzen ist häufig teurer als der nominelle Wert der Münzen, so daß es uninteressant wird, die Münzen herzustellen. Während dieses Konzept beim Schutz vor der Brechung allgemeiner kryptographischer Verfahren in ähnlicher Form anwendbar ist, wird es im MicroMint ganz wörtlich genommen: Die zur Erzeugung von digitalen Münzen nötigen Berechnungen werden bewußt schwierig gestaltet, so daß nur eine befugte Stelle mit genügend großer Computerleistung Münzen produzieren kann. Natürlich kommen noch andere Absicherungen zum Einsatz, damit sich nicht ein finanzstarker Betrüger einen Supercomputer kauft und damit Geld produzieren kann.

An kryptographische Hashfunktionen wird die Forderung gestellt, daß sie möglichst wenig Kollisionen produzieren sollen, d.h. es soll möglichst unwahrscheinlich sein, daß Daten auf den gleichen Wert gehasht werden. Trotzdem kommen solche Kollisionen vor, und genau das macht sicht MicroMint zunutze: Eine MicroMint-Münze besteht im wesentlichen aus Werten x₁,x₂,...,x_k, die alle auf den gleichen Wert gehasht werden, d.h. h(x₁) = h(x₂) = ... = h(x_k). Dies nennt man eine k-Wege-Kollision. Wegen der Unumkehrbarkeit von Hashfunktionen sind diese Kollisionen extrem schwer gezielt zu berechnen, im Grunde bleibt nichts anderes übrig, als einfach so viele Werte auszuprobieren, bis man k Kollisionen gefunden hat. Validieren läßt sich die Münze aber ganz leicht, indem einfach der Hashwert der x₁ bis x_k gebildet und miteinander verglichen wird. Dies läßt sich mit sehr wenig Rechenleistung durchführen, so daß das Verfahren auch für Micropayment geeignet ist.

Wenn die Produktion der Münzen so aufwendig ist, wieso sollte dann jemand überhaupt Münzen herstellen? Nun, der Aufwand nimmt ab, je mehr Münzen produziert werden. Dies ist ähnlich wie beim sogenannten "Geburtstagsparadoxon": Wenn sich eine Menge von m Personen in einem Raum aufhält, wie groß ist dann die Wahrscheinlichkeit, daß zwei Personen am selben Tag Geburtstag haben? Pro Jahrestag, d.h. pro möglichem Paar ist die Wahrscheinlichkeit 1/365. Bei m = 2 gibt es nur ein mögliches Paar, bei m = 3 schon 2, und im allgemeinen Fall m(m - 1) / 2. Die Wahrscheinlichkeit wächst also stark an, und der Effekt ist sogar noch stärker, wenn mehr als zwei Personen am selben Tag Geburtstag haben sollen. Die gleiche Eigenschaft weist auch die k-Wege-Kollision auf: Es ist sehr schwierig, eine einzige k-Wege-Kollision zu finden, aber wenn man dann immer weitere Werte ausprobiert, werden mit der Zeit immer mehr Kollisionen und damit verwendbare Münzen auftauchen.

Damit nur die befugten Stellen von dieser Vereinfachung profitieren, schlagen Rivest und Shamir vor, das ein Verfallsdatum verwendet wird und die Münzen in dieser Zeit zusätzliche Kriterien erfüllen müssen. So ein Kriterium könnte beispielsweise eine bestimmte Eigenschaft der x_i sein. Die Münzen werden im voraus produziert, und das Verfallsdatum sollte so gewählt sein, daß die Zeit seit Bekanntgabe des Kriteriums nicht ausreicht, eine größere Menge Münzen zu erzeugen. Es gibt auch die Möglichkeit, einen Teil der Kriterien geheim zu halten, um einen noch besseren Schutz zu erzielen. Sonst könnten Betrüger über einen langen Zeitraum Münzen erzeugen, in einer Datenbank speichern und einfach erst dann verwenden, wenn die passenden Kriterien veröffentlicht werden.

Wie fast alle Zentralserver-basierten Systeme bietet auch MicroMint keine Anonymität. Die Hauptgefahr ist jedoch, daß eben doch jemand einen Computer zur Verfügung hat, der um Größenordnungen schneller ist als der der befugten Stelle. Dies ist besonders deshalb ein Problem, da die Rechenleistungen ja immer weiter steigen, im Moment noch exponentiell. Wenn allerdings der Wert einzelner Münzen gering gehalten wird und Kontolimitierungen vorgenommen werden, ist ein solcher Angriff nicht besonders lohnend.

5 Fazit

Es gibt eine ganze Reihe von Ansätzen für softwarebasierte E-Cash-Systeme, die nicht auf herkömmlichen Zahlungsmitteln wie Kreditkarten basieren. Einige dieser Ansätze wurden schon in Pilotversuchen erprobt, andere wurden bisher nur auf wissenschaftlicher Ebene diskutiert. Leider ist keinem der Systeme bisher ein durchschlagender Erfolg gelungen. Das liegt zum einen daran, daß zwar die meisten Banken an Feldversuchen mit elektronischem Geld beteiligt sind, aber praktisch jede Bank ein anderes System propagiert. Dies trägt natürlich zu Verunsicherung der Kunden bei. Zu anderen liegt bisher auch noch kein Verfahren vor, daß den Anforderungen von allen Seiten gerecht wird, völlig ausgereift ist und auch noch für alle Arten von Geldtransaktionen geeignet ist. Möglicherweise wird es dieses System auch nie geben, aber wie man am Secret-Splitting-Verfahren für die Lösung des Double-Spending-Problems oder an MicroMint und PayWord erkennen kann, ist durchaus noch Spielraum für weitere Entwicklungen gegeben. Zur Zeit gibt es jedenfalls die Tendenz, für unterschiedliche Aufgaben unterschiedliche Verfahren zu propagieren, d.h. insbesondere für kleine Transaktionssummen die Micropaymentverfahren.

Obwohl die Einführung von elektronischem Geld eher schleppend anläuft, werden wir längerfristig wohl nicht darum herumkommen. Der Bedarf ist auch jetzt schon da und wird im Zeitalter des vielzitierten "globalen Dorfes" und des weltweiten Zusammenwachsens immer mehr zunehmen. Gerade der Handel, aber auch andere Industrien haben ein großes Interesse am elektronischen Handel. Möglicherweise wird in nicht allzu ferner Zukunft die Bezahlung mit elektronischem Geld die Regel sein und die Bezahlung mit Scheinen, Münzen und vielleicht sogar Kreditkarten die Ausnahme.

Literatur

[1] Bruce Schneier. Applied Cryptography, John Wiley & Sons, 1996

[2] Peter Wayner. Digital Cash, Commerce on the net, 2nd Edition. Academic Press, 1998

[3] Papers and Documentation for NetCash and NetChaque. http://nii.isi.edu/info/netcheque/documentation.html

[4] DigiCash Inc. Electronic Payments With ecash. http://www.digicash.com/ecash/docs/index.html

[5] David Chaum. Security without Identification:Card Computers to make Big Brother Obsolete. 1987. http://www.digicash.com/news/archive/bigbro.html

[6] Ellis Chi. HP Labs Technical Reports: Evaluation of Micropayment Schemes. 1997. http://www.hpl.hp.com/techreports/97/HPL-97-14.html

[7] Compaq Computer Corp. The MilliCent Protocol for Inexpensive Electronic Commerce. http://www.millicent.digital.com/works/details/index.html

[8] CyberCash Inc. http://www.cybercash.com

[9] Ronald Rivest, Adi Shamir. PayWord and MicroMint: Two simple micropayment schemes. http://theory.lcs.mit.edu/~rivest/RivestShamir-mpay.ps

---